4. Graph Theory & Algorithm
Coursera에서 제공하는 C++ for C programer 를 보고 포스팅을 하고 있습니다. :)
언어를 익히는 것만큼 중요한 것이 바로 알고리즘이다. 언어는 문제를 해결하기 위한 도구이고 이 도구를 잘 사용하여 문제를 해결하는 능력을 길러야한다. 그래프 이론은 많은 문제에서 사용되고 있는 이론인데, 네비게이션을 이용하여 경로를 검색한다던지, 인공지능 분야등 정말 여러 분야에 걸쳐 이론이 사용되고 있다. 이 그래프를 data type으로 표현해보고 이를 통해 C++를 더 깊게 이해해보자.
그래프를 자료구조로 나타내는 방법은 여러가지가 있다.
- Connectivity matrix (also distance)
- Edge List Representation
- Tradeoffs - Graph as an ADT
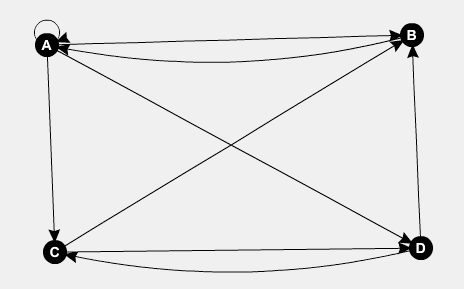
N개의 꼭지점을 가진 유향그래프 는 List Representation으로 표현할 수 있다.
- 정의 : n개의 꼭지점을 지나는 유향그래프를 n개의 꼭지럼 리스트로 이뤄진 배열로 표현하는 것
- 만약 꼭지점 i에서 j로 가는 길이 이싿면 리스트 i가 꼭지점 j를 포함한다.
- 엣지에 가중치가 있다면 꼭지점 / 가중치 쌍으로 표현한다.
- 무향그래프에서 i에서 j로 가는 길이 있다면 리스트 i와 j모두 표시한다.
Matrix vs. list directed Graph
그래프를 적절한 자료로 나타내면 다음과 같다.
- Matrix
| A | B | C | D | |
|---|---|---|---|---|
| A | 1 | 1 | 1 | 1 |
| B | 1 | 0 | 0 | 0 |
| C | 0 | 1 | 0 | 1 |
| D | 0 | 1 | 1 | 0 |
- list directed Graph
A -> A -> B -> C -> D
B -> A
C -> B -> D
D -> B -> CDijkstra Shortest Path
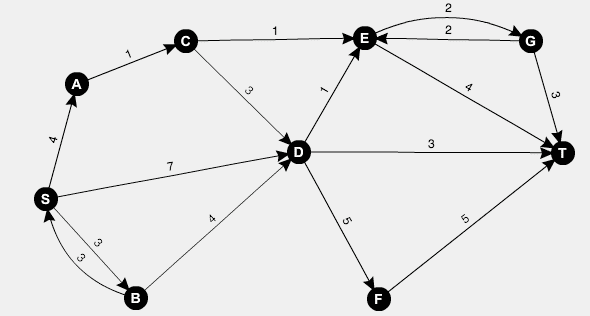
다익스트라 알고리즘은 어떤 변(Edge)도 음수 가중치를 갖지 않는 유향 그래프에서 주어진 출발점과 도착점 사이의 최단 경로 문제를 푸는 알고리즘이다. 실생활에서 각 꼭지점이 도시를 나타내고 변들이 도로를 나타낸다면 알고리즘을 통해 최단 경로를 찾을 수 있다.
- 단계 1 - 닫힌 집단에 있는 노드 s와 열린 집단에 있는 s바로 다음에 오는 노드와의 거리를 포함한다.
-
단계 2
- 열린 노드중 가장 가중치가 작은것을 고른다. 이 노드를 n이라고 하자.
- 선택된 노드가 d라면 멈춘다.
- 그렇지 않다면, 다음에 올 모든 노드 n에 대해서 계산한다.
- s에서부터 n 까지와 n에서 부터 k까지의 거리를 더한다.
- 그거리가 가장 작다면 그 노드를 선택하고 위 과정을 반복한다.
다익스트라 알고리즘이 끝나는 조건은 다음과 같다.
- 선택된 노드가 d 일 경우
- 다음 노드가 없을 경우 (경로 찾기 실패)
- 최단 경로를 찾았을 때
그럼 알고리즘 대로 S에서 T까지 찾아가보자.
S 에서 시작해보자. S 에서 갈 수 있는 곳은 A, B, D 이다. S에서 각 노드로 가는 비용은 아래와 같다.
| S | |
|---|---|
| A | 4 |
| B | 3 |
| D | 7 |
이중에서 가중치가 가장 작은것은 B이므로 B를 선택한다. B에서 S로 갈 수 있는 길이 있지만 이미 S는 닫힌 집합에 포함되어 있으므로 선택하지 않는다. B에서 D까지 가는 길은 4이므로 S에서 D까지 가는 길은 3 + 4가 되어 7이 된다. 위에서 S에서 바로 D까지 가는 길과 같은 값을 가지므로(개선되지 않으므로) 업데이트 되지 않는다.
그다음 열린 집합에서 가장 작은변은 S에서 A로 가는 변이다. 이 변의 가중치는 4이다. A에서 갈 수 있는 곳은 C이므로 S에서 C까지는 가중치 5이다. C노드에서는 D와 E로 갈 수 있는데 5에 엣지 CD의 가중치를 더하면 8이 되므로 이전 최소값보다 크므로 업데이트되지 않는다. 하지만 C에서 E로 갈 수 있다. S부터 E까지는 6의 비용으로 방문 할 수 있다. E에서 T로 가면 가중치 10으로 방문 할 수 있다.
최단 경로임을 확인해야 하므로 SDT를 지나는 경로의 비용, E에서 G를거쳐 T를 방문하는 비용을 비교하면 된다.