김로그

4.Binary Tree Traveral에 대해 알아보자

예전에 대학원 입학시험을 볼 때 Binary Tree Traversal 문제가 나왔었다. 멍청하게도 postorder 랑 preorder 가 헷갈려서 틀렸었다.
다시는 이런일이 없도록 이번 포스팅에서는 Binary Tree Traversal 에 대해 알아보도록하자. 아이러니하게도 대학원에 합격했었다. -_ -;

배열과 같은 선형 데이터구조를 방문 하는 방법은 처음부터 끝까지 혹은 뒤에서부터 첫 원소까지 방문하는 방법이 있다. 그리고 나중에 포스팅할 그래프에서는 dfs, bfs 로 노드들을 방문할 수 있다. tree 특히 binary tree 에서는 트리순회(tree traversal)로 노드들을 방문 할 수 있는데 본격적으로 트리순회에 대해서 알아보기전에 트리순회의 정의에 대해서 알아보자.

정의

Tree의 Node들을 지정된 순서대로 “방문”하는 것

만약 왼쪽 자식노드를 L 지금 노드를 N 오른쪽 자식노드를 R 이라고 하면 총 여섯가지의 방문 순서가 있게된다. LNR LRN …등등
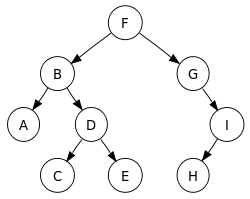현재 노드에 따른 왼쪽 자식노드와 오른쪽 자식노드 방문순서에 따라 각각

  • preorder(전위순회)가 있다.
  • inorder travesal(중위순회)
  • postorder traversal(후위순회)
  • 그리고 level-order

preorder traversal (전위순회)

preorder traversal 은 루트 노드에서부터 다음과 같은 방법으로 노드들을 방문한다.

  • 노드를 방문한다.
  • 왼쪽 서브트리를 전위 순회한다.
  • 오른쪽 서브트리를 전위 순회한다.

즉 노드를 먼저 방문하고 왼쪽 끝까지 내려간 다음 오른쪽으로 이동하여 다시 시작하거나 오른쪽으로 이동하여 순회를 계속하게 된다.
방문순서 F > B > A > D > C > E > G > I > H

inorder traversal (중위순회)

  • 왼쪽 서브트리를 중위순회한다.
  • 노드를 방문한다.
  • 오른쪽 서브트리를 중위순회한다.

왼쪽 끝까지 내려간 이후 노드를 방문하고 오른쪽 자식노드로 이동하여 순회를 계속하게 된다.
방문순서 A > B > C > D > E > F > G > H > I

postorder traversal (후위순회)

- 왼쪽 서브트리를 후위순회한다. - 오른쪽 서브트리를 후위 순회한다. - 노드를 방문한다.

방문순서 A > C > E > D > B > H > I > G > F

위 traversal들을 코드로 나타내면 아래와 같다.

void traversal(node){
  if(node){
    //visit(node); preorder
    traversal(node->left);
    //visit(node); inorder
    traversal(node->right);
    //visit(node); postorder
  }
}

각각에 해당하는 traversal의 visit함수만 남겨놓고 삭제하면되는데 생긴대로 함수가 구현되어있어서 기억하기 쉽다.
또 위 세 순회들이 재미있는 점은 수식에서 전위표기(prefix), 중위표기(infix), 후위표기(postfix)에 대응된다는 점이다.

levelorder traversal

root 부터 한 레벨씩 아래로 이동하는 level order 는 queue 를 이용하여 구현할 수 있다.

levelorder(root)
  q ← empty queue
  q.enqueue(root)
  while (not q.isEmpty())
    node ← q.dequeue()
    visit(node)
    if (node.left ≠ null)
      q.enqueue(node.left)
    if (node.right ≠ null)
      q.enqueue(node.right)

출처 wikipedia

reference