Coursera에서 제공하는 Machine learning by Andrew ng 을 보고 포스팅하였습니다.

단순 선형 회귀는 하나의 입력에 대한 결과를 예측한다. 이번 포스팅에서는 집값 에측과 비용함수에대한 개념 그리고 gradient descent방법에 대해서 알아본다.

모델표현(model representation)

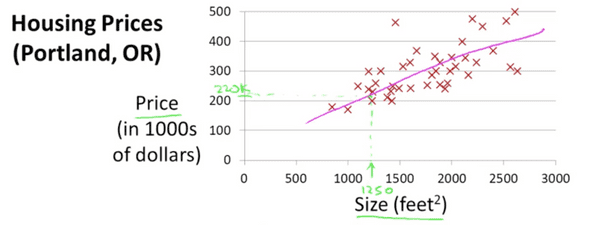
친구가 집을 팔려고하는데 얼마에 팔아야하는지 잘 모른다. 이런 경우 지도학습(supervised learning) 알고리즘을 사용해야하고 회귀(regression) 문제임을 이미 알고있다. 왜냐하면 우리가 궁금해하는 면적당 집값에 대한 데이터를 이미 알고 있고, 친구 집 면적에 대한 가격이 궁금하기 때문이다.

그림의 오른쪽에 실제 판매된 면적당 가격 표가 있다. 이것을 training set 이라고 하자. Training set에 다양한 집들의 가격이 나타나있다. 이 데이터를 통해서 알고리즘을 학습시키고 최종적으로 학습한 알고리즘을 통해 집 값을 예측하는 것이 이 문제의 목표이다. 문제를 풀기전에 먼저 몇가지 심볼들을 정의하자

Notation:

• m = 트레이닝 예(trading example)의 갯수
• x’s = “입력변수” / 특징들
• y’s = “출력”변수 / “목표(target)“변수
• $(x, y)$ 한 쌍의 트레이닝 예
• $(x^{(i)},y^{(i)})$ i 번째 행의 트레이닝 예

이제 지도학습 알고리즘이 어떻게 작동하는지 알아보자

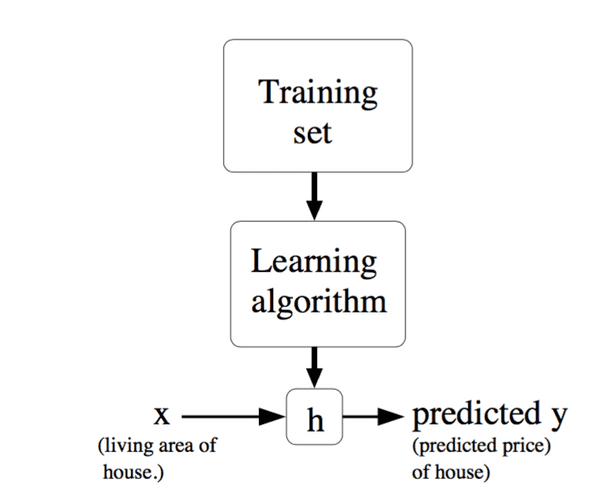
우리가 이미 알고있는 데이터, 트레이닝 셋(training set) 을 학습 알고리즘(learning algorithm) 에 넘거주면 알고리즘은 데이터를 학습을 하여 하나의 가설함수(hypothesis function) 를 만든다.

만들어진 가설함수를 통해 집의 크기에 대한 집 가격을 예측할 수 있다.

나도 처음에 수업을 들을 때 왜 hypothesis function이라고 하는지 궁금했다. 사실 뜻을 몰랐다. 수업을 하시는 엔드류 응 교수님은 이름이 적절하지 않으니 이름에 너무 연연하지 말라고 하셨다.

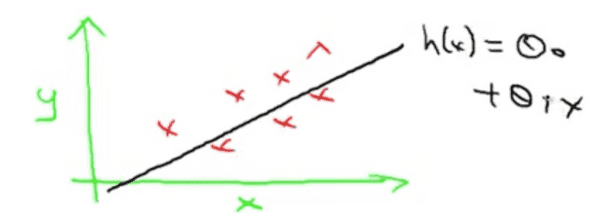
그 다음으로 해야하는 일은 가설함수 표현이다. 일반적으로 가설함수 h 는 다음과 같이 표현한다.

가설함수 표현을 간단하게 하기위해서 $h(x)$로 표현하기도 한다. 가설함수는 위에서 설명했듯이 x에 대한 y값을 예측한다.

이러한 선형 모델을 Linear Regression with One Variable 라고 하고 좀더 세련된 표현으로 Univariate Linear Regression 이라고 한다. 우리말로는 단순 선형 회귀 라고 한다.

비용함수(Cost Function)

어떤 직선이 데이터들을 가장 잘 나타내는지 알아보자.

단순 선형회귀에서 $\theta_i$ 를 회귀 모델의 매개변수(parameter)라고 하자. $\theta_i$에 따라 가설함수가 결정된다. 그럼 어떤$\theta_0$과 $\theta_1$을 선택해야 트레이닝 셋을 가장 잘 표현하는 가설함수를 얻을 수 있을까?

트레이닝 셋의 y와 $h(x)$ 의 차이가 가장 작도록 $\theta$를 고르는것이 가설함수가 트레이닝 셋을 가장 잘 표현할것이다.

그럼 가설함수가 데이터를 잘 표현하는지 어떻게 알 수 있을까? 바로 비용함수(cost function) 을 이용하면 가설함수의 정확성을 알 수 있다. 비용함수는 x에 대한 가설함수의 결과 $h(x^{(i)})$ 와 실제 결과 y의 차이의 평균을 구한다.

평균을 구한다면 $m$으로 나눠야 하는데 $2m$으로 나누었다.

이 수업의 멘토는 이렇게 설명해주셨다.[link]

This is simply a mathematical convenience, so that it cancels with the ‘2’ that appears in the numerator from the partial derivative equation. - Tom Mosher

나중에 계산의 편의를 위해 편미분 후 분자에 나타나는 2를 상쇄시키기 위해서 2m으로 나눈다고 한다.

비용함수는 Squared error function 혹은 Mean squared error라고 불리기도 한다.

비용함수를 통해 가설함수가 얼마나 데이터들을 잘 표현하는지 알 수 있다. 비용함수의 결과를 최소로 만드는 $\theta$값을 찾아야하는데 이를 minimization problem 이라고 한다.

Gradient Descent

비용함수를 최소화 하기위해 Gradient Descent 알고리즘을 사용한다 Gradient Descent는 선형회귀 문제뿐만 아니라 머신러닝 전반에 사용되는 알고리즘이라고 한다.

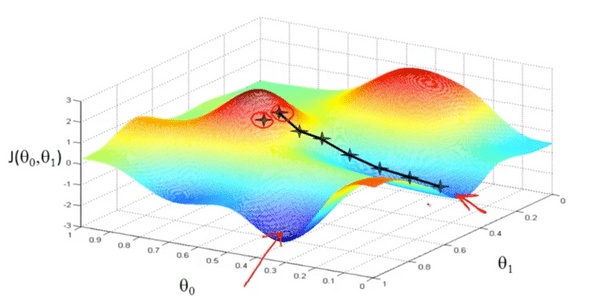
$\theta$값에 따른 비용함수의 값은 위와 같은 그래프를 그릴 것이다. 비용함수를 최소화하는 값을 찾는것이 가장 좋은 가설함수를 찾는것이고 이것이 Gradient Descent알고리즘의 목표이다.

Gradient Decent알고리즘을 살펴보자

gradient descent equation

• := ** : **대입연산 이다 오른쪽의 결과를 왼쪽으로 대입한다는 뜻이다. 프로그램 언어의 =와 같은 기능을한다.
• $\alpha$ : 학습주기(Learning Rate), 알파값이 클 수록 변화의 폭이 크고, 알파의 값이 작을수록 변화의 폭이 작아진다.
• $\alpha$뒤의 수식 : 미분텀(derivarate term) $\alpha \frac{\partial} {\partial \theta_j} J(\theta_0, \theta_1)$

Gradient Decent는 J=0, J=1일 때를 동시에 업데이트를 한다.

위 과정을 반복하다보면 미분텀은 0이 될것이고 최종적으로 우리가 원하는 $\theta$값을 찾을 수 있다.

그럼 위의 수식이 어떻게 최소점을 찾는지 알아보자

우선 미분텀을 살펴보면 그래프의 특정점에 대한 기울기임을 알 수 있다. 현재 위치에서 미분값이 양수이면 현제 위치에서 증가하는 중이고 그 값을 a와 곱해서 빼면 $\theta$값은 감소하게 되고 최소점에 가까워지게 된다. 반대로 미분텀의 값이 음수이면 현재위치에서 기울기가 음수이므로 감소하는 중이다 $\theta$에서 음수를 빼면 업데이트된 $\theta$는 증가하므로 최소점에 가까워진다.

그럼 $\alpha$값에 따라 gradient decent는 어떻게 변할까? $\alpha$값이 너무 작으면 $\theta$의 값이 아주 조금씩 변할 것이다. $\alpha$의 값이 너무 크다면 overshooting이 일어나 아마 최소점을 찾지 못 할 수도 있다.

Gradient Descent for Linear Regression

이제 비용함수를 최소화하기 위해 Gradient Decent 알고리즘을 사용해보자

여기서 핵심이 되는 것은 Gradient Decent의 미분텀이다. 위 과정을 잘 정리하면 아래와 같이 나타낼 수 있다. [참조]