김로그

3.Logistic Regression

Coursera에서 제공하는 Machine learning by Andrew ng 을 보고 포스팅하였습니다.

Classification

이메일이 스펨인지 아닌지 온라인 매물이 허위매물인지 아닌지 구분하는 것 처럼 데이터를 어떤 기준에 의해 분류하는 문제를 분류문제(classification problem)이라고 한다.

그럼 Classification 알고리즘을 어떻게 만들까? 이전에 다루었던 종양 문제를 다시 살펴보자.

ml3 0

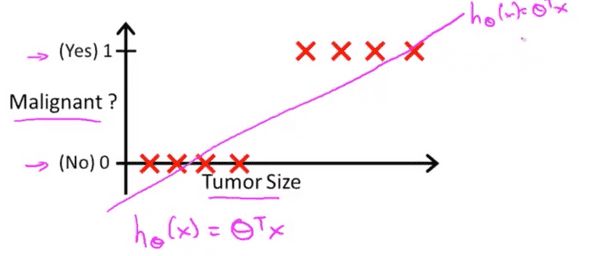
종양 크기에 따라 악성종양인지 아닌지 구분하였다. 앞서 배운 Linear regression으로 모델을 표현하는 가설함수를 만들면 아마 분홍색 실선이 될 것이다. 이 문제에 대해서 예측을 하려고 한다면 가설함수의 y축이 0.5보다 크면 악성, 0.5보다 작으면 악성이 아님으로 기준을 잡을 수 있다.

ml3 1

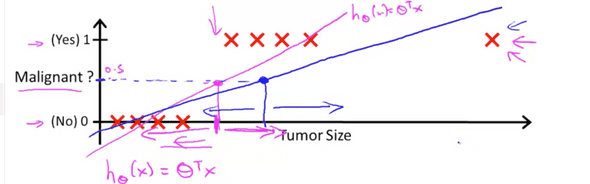
이 모델에 오른쪽에 파란색 화살표로 표시한 원소를 하나 추가 시키자. 딱히 이 모델이 바뀌진 않았지만 이 모델을 가장 잘 표현하기 위해 비용함수(cost function)의 값이 작아지는 쪽으로 가설함수가 만들어질 것이고 그렇다면 위의 파란색 실선처럼 가설함수를 표현할 수 있다. 앞에서 했던것과 같이 한계점(threshold)를 0.5로 잡으면 가설함수의 y축이 0.5가 되는 x의 좌표를 기준으로 데이터들을 분류(classify)할 수 있을것이다. 그렇게 된다면 경우에 따라, 특히 이 경우에는 잘못 분류되는 데이터들이 생기게 된다. 이 경우 linear regression을 적용했을때 나타나는 안좋은 경우 중 하나이다.

경우에 따라 운이 좋아서 linear regression이 모델을 잘 표현할 때도 있지만 보통은 그렇지 않으므로 Andrew Ng교수님은 classification문제에 linear regression을 사용하지 않는다고 하신다.

만약 classcification을 통해 y가 0 또는 1 로 분류하고 싶을 때 linear regression의 가설함수 h(x)는 0보다 작거나 1보다 큰 경우가 있어 적절하지 않다.

이 문제를 해결하기 위해 가설함수(hypothesis function) 의 값이 0과 1사이인 Logistic Regression 에 대해서 알아보도록 하자. Regression이란 이름이 나와서 당황스러울수도 있지만 Logistic Regression 알고리즘은 사실 classification문제에 사용하는 알고리즘 중 하나이다.

Hypothesis Representation

그럼 분류(classification) 문제에서 가설함수(hypothesis function) 를 어떻게 표현하는지 알아보자.

범위가 0≤hθ(x)≤10 \leq h_\theta (x) \leq 1 인 logistic model을 표현하는 가설함수는 hθ(x)=g(θTx)h_\theta (x) = g ( \theta^T x ) 로 표현한다.

linear regression의 가설함수와 비교하면 g()g() 가 θTx\theta^Tx (linear regression의 가설함수)를 감싸고있는걸 알 수 있다.

g(z)=11+e−zg(z) = \dfrac{1}{1 + e^{-z}} 는 sigmoid function 혹은 logistic function 이라고 한다.

sigmoid function

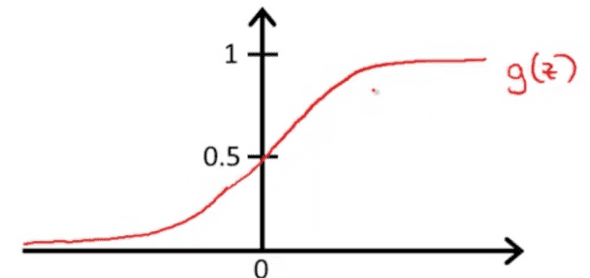
sigmoid function은 g(z)와 z축에 각각 1, 0에 점근선이 그려진다.

Decision Boundary

그럼 분류문제에서 logistic function을 이용해서 어떻게 분류를 할까

0 혹은 1 분류에서 가설함수의 결과에 따라서 0, 1을 분류하면 된다.

hθ(x)≥0.5→y=1hθ(x)<0.5→y=0\begin{aligned} & h_\theta(x) \geq 0.5 \rightarrow y = 1 \\ & h_\theta(x) < 0.5 \rightarrow y = 0 \\ \end{aligned}

decision boundary

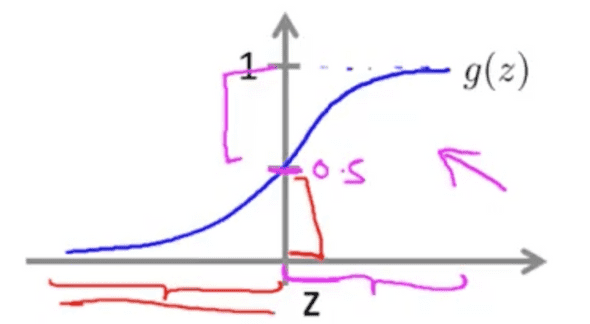
logistic function에서 z가 0보다 크면 g(z)는 항상 0.5보다 크다. 그리고 z가 0보다 작으면 항상 g(z)는 0.5보다 작다. 자연로그의 특성을 이용해서 logistic function의 성질을 정리하면

z=0,e0=1,g(z)=1/2z→∞,e−∞→0,g(z)=1z→−∞,e∞→∞,g(z)=0\begin{aligned} z=0, e^{0}=1, g(z)=1/2 \\ z \to \infty, e^{-\infty} \to 0, g(z)=1 \\ z \to -\infty, e^{\infty}\to \infty, g(z)=0 \end{aligned}

가 된다. logistic function의 입력 zz 는 θTx\theta^Tx 이므로

hθ(x)=g(θTx)≥0.5when  θTx≥0\begin{aligned} & h_\theta(x) = g(\theta^T x) \geq 0.5 \\ & when \; \theta^T x \geq 0 \end{aligned}

따라서

θTx≥0→y=1θTx<0→y=0\begin{aligned} & \theta^T x \geq 0 \rightarrow y = 1 \\ & \theta^T x < 0 \rightarrow y = 0 \\ \end{aligned}

가 된다. 수식이 많아서 복잡해 보이지만 마지막 결론만 알고 있으면 될 것 같다.

Cost function

아쉽게도 Linear regression에서 사용했던 비용함수(cost function) 을 사용할 수 없다. 그 이유는 linear regression의 비용함수를 사용하면 결과가 너무 구불구불(wavy)하게 나오기 때문이다. 그렇게 되면 지역 최적점(local optima)가 생겨 전역 최소점(global minimum)을 찾기 어려워진다. 맞게 해석한건지 모르겠다. 다르게 설명하자면 linear regression의 비용함수를 사용하면 볼록한 함수(convex function)가 되지 않기 때문이다.

logistic regression에서 사용하는 비용함수는 아래와 같다.

J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))Cost(hθ(x),y)=−log⁡(hθ(x))  if y = 1Cost(hθ(x),y)=−log⁡(1−hθ(x))  if y = 0\begin{aligned} & J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \\ & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{if y = 1} \\ & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{if y = 0} \end{aligned}

y가 1과 0 일때 h(x)는 이렇게 된다.

sigmoid function

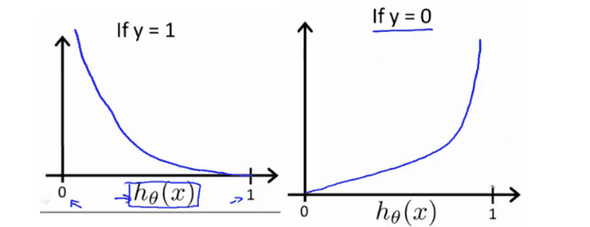
logistic regression에서 비용함수의 특징은 아래와 같다.

Cost(hθ(x),y)=0 if hθ(x)=yCost(hθ(x),y)→∞ if y=0  and  hθ(x)→1Cost(hθ(x),y)→∞ if y=1  and  hθ(x)→0\begin{aligned} & \mathrm{Cost}(h_\theta(x),y) = 0 \text{ if } h_\theta(x) = y \\ & \mathrm{Cost}(h_\theta(x),y) \rightarrow \infty \text{ if } y = 0 \; \mathrm{and} \; h_\theta(x) \rightarrow 1 \\ & \mathrm{Cost}(h_\theta(x),y) \rightarrow \infty \text{ if } y = 1 \; \mathrm{and} \; h_\theta(x) \rightarrow 0 \\ \end{aligned}

Simplified Cost Function

logistic function의 비용함수를 표현할 때 아래의 표현이 있었다. 이를 좀 더 간단하게 표현해보자.

Cost(hθ(x),y)=−log⁡(hθ(x))  if y = 1Cost(hθ(x),y)=−log⁡(1−hθ(x))  if y = 0\begin{aligned} & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{if y = 1} \\ & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{if y = 0} \end{aligned}

이를 좀 더 간단하게 나타내면 아래와 같다.

Cost(hθ(x),y)=−y  log⁡(hθ(x))−(1−y)log⁡(1−hθ(x))\begin{aligned} \mathrm{Cost}(h_\theta(x),y) = - y \; \log(h_\theta(x)) - (1 - y) \log(1 - h_\theta(x)) \end{aligned}

위 두 표현에서 y는 0 혹은 1이 되는 경우만 존재하기 때문이다.(classfication) y가 1일 때는 위 표현의 (1−y)log⁡(1−h(x))(1 - y) \log(1 - h(x)) 가 소거 되고, y가 0일 때는 −y  log⁡(h(x))- y \; \log(h(x)) 항이 소거 된다.

그럼 logistic regression에서 비용함수는 다음과 같이 표현할 수 있다.

J(θ)=−1m∑i=1m[y(i)log⁡(hθ(x(i)))+(1−y(i))log⁡(1−hθ(x(i)))]\begin{aligned} J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] \end{aligned}

벡터 표현은 아래와 같다.

J(θ)=−1m(log⁡(g(Xθ))Ty+log⁡(1−g(Xθ))T(1−y))\begin{aligned} J\left(\theta\right) = -\frac{1}{m}\left(\log\left(g\left(X\theta\right)\right)^{T}y+\log\left(1-g\left(X\theta\right)\right)^{T}\left(1-y\right)\right) \end{aligned}

Gradient descent

J(θ)=−1m∑i=1m[y(i)log⁡(hθ(x(i)))+(1−y(i))log⁡(1−hθ(x(i)))]\begin{aligned} J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] \end{aligned}

비용함수 J(θ)J(\theta) 를 최소로 하는 θ\theta 값을 찾기 위해 Gradient descent 알고리즘을 수행한다. linear regression에서 했던 것을 생각하면 Gradient descent의 일반표현은 아래와 같다.

Repeat  {  θj :=θj−α∂∂θjJ(θ)(simultaneously update all θJ)}\begin{aligned} & Repeat \; \lbrace \\ & \; \theta_j := \theta_j - \alpha \dfrac{\partial}{\partial \theta_j}J(\theta) \\ & (simultaneously\ update\ all\ \theta_J )\\ & \rbrace \end{aligned}

α\alpha 뒤의 미분항을 잘 정리하면 logistic regression에 대한 gradient descent는 아래와 같다.

Repeat  {  θj :=θj−αm∑i=1m(hθ(x(i))−y(i))xj(i)}\begin{aligned} & Repeat \; \lbrace \\ & \; \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \\ & \rbrace \end{aligned}

겉보기엔 linear regression과 같은 알고리즘으로 보이지만 linear regression과 logistic regression의 가설함수가 다르므로 다른 결과가 나온다.

advanced Optimization

최적의θ\theta 를 구하기 위해서는 다음 두식을 풀어야한다.

J(θ)∂∂θjJ(θ)\begin{aligned} & J(\theta) \\ & \dfrac{\partial}{\partial \theta_j}J(\theta)\end{aligned}

최적의 θ\theta 를 구하는 방법은 gradient descent알고리즘 뿐만 아니라

등 다양한 알고리즘이 존재한다.

Gradient descent알고리즘과 비교했을 때 위 세 알고리즘의 장점은 α\alpha (learning rate)를 선택하지 않아도 된다는 점과 gradient descent알고리즘보다 빠른경우가 많기 때문이다. 단점은 알고리즘이 gradient descent보다 복잡하지만 구현에 있어 많은 머신러닝 라이브러리에 관련 알고리즘이 구현되어 있으므로 해당 알고리즘을 사용하면 된다.

Multiclass Classification:One vs All

Multiclass classification란 무엇일까? 말 그대로 다중 분류이다. 한국말로하니까 더 어렵다, 이전의 분류문제에서는 y가 0,1인 두가지 분류만 고려했으나 다중 분류에서는 y가 0,1,2…으로 나누는 문제를 푼다. 이를테면 이메일이 왔는데 친구에게 온 메일, 회사에서 온 메일, 스펨메일 등등으로 나누는 문제가 다중 분류 문제이다.

sigmoid function

One vs All은 n개의 원소에 대해서 n+1개의 binary classification 문제를 푼다. 위 그림과 같이 3부류로 나눌 때 그 부류에 속하는것, 아닌것으로 분류하는 문제를 반복한다. 하나의 분류 문제를 풀고 그에 대한 확률을 y라고 할 때

y∈{0,1...n}hθ(0)(x)=P(y=0∣x ;θ)hθ(1)(x)=P(y=1∣x ;θ)⋯hθ(n)(x)=P(y=n∣x ;θ)prediction=max⁡i(hθ(i)(x))\begin{aligned} & y \in \lbrace0, 1 ... n\rbrace \\ & h_\theta^{(0)}(x) = P(y = 0 | x ; \theta) \\ & h_\theta^{(1)}(x) = P(y = 1 | x ; \theta) \\ & \cdots \\ & h_\theta^{(n)}(x) = P(y = n | x ; \theta) \\ & \mathrm{prediction} = \max_i( h_\theta ^{(i)}(x) )\\ \end{aligned}

가 된다.

Reference