김로그

4.Regularization

Coursera에서 제공하는 Machine learning by Andrew ng 을 보고 포스팅하였습니다.

The problem of overfitting

이전 포스팅에서 Linear Regression, Logistic Regression을 통해 Regression문제와 Classification문제를 풀 수 있음을 알아 보았다. 이 두 알고리즘은 꽤 많은 기계학습 문제를 풀 수 있다. 하지만 이러한 기계학습 응용프로젝트는 종종 과적합 문제(overfitting problem) 문제를 야기한다. 이번 포스팅에서는 정규화(Regularization) 를 통해 과적합 문제를 해결하는 방법에 대해서 알아보자.

시작하기 앞서 과적합(overfittin) 이란 무엇인지 짚고 넘어가자.

선형회귀(Linear Regression)에서 과적합을 알아보자

ml4 0

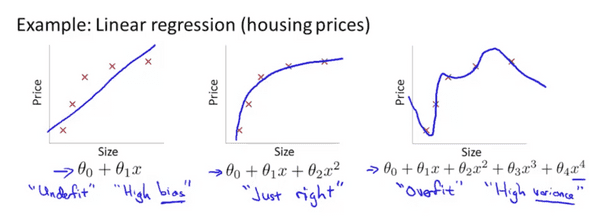
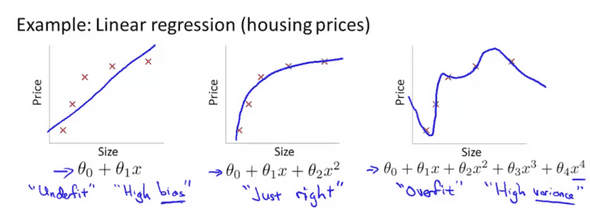
같은 모델을 각각 다른 가설함수(hypothesis function)으로 나타냈다. 가장 왼쪽에 1차함수로 표현한 모델은 사이즈가 증가함에 따라 가격이 증가하는 것을 잘 표현했지만 데이터 모델(training data model) 에 대해서 정확하게 표현했다고 하기 어렵다. 이런 경우를 Underfit 이라고 하고 다른 말로 High bias 라고 한다.

가장 오른쪽의 표현을 살펴보자. 각각의 데이터 모델에 대하여 정확하게 표현되었지만 곡선이 요동치는 것을 볼 수 있다. 직관적으로 집 가격 모델을 잘 표현했다고 하기 어렵다. 이런 경우를 과적합(overfitting) 이라고 하며 다른 말로 hight varience 라고 한다.

가운데 처럼 모델을 잘 표현한 경우는 딱히 이름이 없지만 just right이라고 하자. 가운데 경우 직관적으로 보았을 때 집 모델을 잘 표현했다고 할 수 있다.

개인적인 생각이지만 2차 함수로 모델을 표현했을 경우 사이즈가 증가함에 따라 가격이 낮아지는 구간이 생기므로 딱히 잘 표현하긴 어렵지만 주어진 데이터 모델에 대한 표현이 적절하므로 비교하기 좋은 대상이라서 교수님이 이런 그림을 그리신것 같다.

오른쪽의 경우와 같이 너무 많은 특징(θ\theta)들로 모델을 표현할 경우 가설함수(hypothesis)는 주어진 데이터(training set)에 너무 딱 맞게 된다. 이런 경우 수식으로 비용함수가 거의 0에 가깝거나 0이 되며 새로운 데이터에 대해서 일반화를 실패 할 수 있다. 혹은 새로운 데이터에 대한 가격 예측을 실패할 수 있게된다.

ml4 1

Logistic Regression에서도 마찬가지로 가장 왼쪽의 모델표현은 썩 잘 표현했다고 하긴 어렵다. 가장 오른쪽 모델 표현은 주어진 데이터에 대해서 모두 만족하지만 새로 데이터를 추가하여 분류하기엔 어려움이 있다.

그럼 과적합(overfitting)문제는 아래와 같은 방법으로 풀 수 있다.

  • 특징의 수를 줄인다.

    • 주요 특징을 직접 선택하고 나머지는 버린다.
    • Model selection algorithm을 사용한다.

  • Regularization

    • 모든 특징을 사용하나 특징 θj\theta_j에 대한 parameter를 줄인다.

이번 포스팅에서는 Regularization을 통한 overfitting 해결에 대해서 다루고 model selection algorithm은 다른 포스팅에서 다루도록 하겠다.

Cost function

Quardratic Linear Regression의 hypothesis θ0+θ1x+θ2x2+θ3x3+θ4x4\theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4 가 있고 overfitting문제가 있다고 가정하자. 그리고 우리는 θ3x3\theta_3x^3과 θ4x4\theta_4x^4 의 영향을 줄여 overfitting 문제를 개선하고자 한다 어떻게 하면 될까?

아이디어는 바로 비용함수(cost function) 을 바꾸는 데에 있다. 알다시피 비용함수는 가설함수의 각항의 개수가 되는 최적의θ\theta를 구하는 식이다. 가설함수의 표현을 바꾸거나 몇몇 특징을 포기하는 대신 비용함수를 수정함으로써 과적합을 개선할 수 있다. 위 문제의 경우 아래와 같은 비용함수를 사용하면 될 것이다.

minθ 12m∑i=1m(hθ(x(i))−y(i))2+1000⋅θ32+1000⋅θ42min_\theta\ \dfrac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + 1000\cdot\theta_3^2 + 1000\cdot\theta_4^2

2차원의 평면에 그려지는 그래프에서 θ\theta항의 차수가 크면 클수록 구불구불해지는 성질이 커진다. 따라서 이런 성질을 최소화하기 위해서 각각 1000을 곱해줬다. 이렇게 비용함수를 통해서 나오게 되는 x3x^3과 x4x^4의 계수 θ\theta는 0에 가까워 지게 되고 구불구불하게 나타나는 성질은 줄어들게 된다. 그렇게 되면 기존에 주어진 식은 거의~~

θ0+θ1x+θ2x2\theta_0 + \theta_1x + \theta_2x^2

꼴이 되고 아주 약간의 x3x^3와 x4x^4가 더해진 꼴이 된다.

위 예에서는 x의 3,4차 항의 계수인 θ\theta들만 regularize를 했지만 사실은 모든 특징 즉 모든 xnx^n의 계수에 대해서 regularize를 해야한다고 한다. 이유는 이해하기 어렵다고 설명안해주셨지만 해보면 안다고 하셧다.. 시크해..

여튼 일반적으로 나타내면

minθ 12m [∑i=1m(hθ(x(i))−y(i))2+λ ∑j=1nθj2]min_\theta\ \dfrac{1}{2m}\ \left[ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\ \sum_{j=1}^n \theta_j^2 \right]

가 된다. 여기서 눈 여겨 볼점은 두번째 항인 람다 어쩌고 인데 0이 아닌 1부터 시작한다는 점이다. 사실은 실제 문제를 풀때는 상수항도 regularize를 해야할 경우도 있으므로 모든 θ\theta에 대해서 regularize를 해야한다. (내가 잘 못 알아들은 것같기도 하고…)

여튼 Regularization을 통해 더 간단한 가설함수를 도출해 낼 수 있고 과적합 문제도 해결할 수 있다. 위에 비용함수식에서 두번째 항을 Regularization Term 이라고 하고 λ\lambda를 Regularization Parameter 라고 한다.

비용함수식의 각 항의 역할에 대해서 알아보도록 하자. 첫번째 항 그러니까 우리가 익숙히 보던 원래 비용함수꼴은 데이터 셋(training set)에 대해서 잘 맞게(fit) 함수를 훈련시키는 것이다. 두번째 Regularization Term의 역할은 각항의 계수를 작게 만들어 가설함수를 간단하게 하고 과적합을 피하게 한다.

그렇다면 λ\lambda가 너무 클 경우 어떻게 될까? 이를 테면 막 101010^10정도 된다고한다면… 아마 상수항을 제외한 모든 항의 계수는 0에 가까워 질 것이고 이로 인해 도출되는 비용함수는 거의 상수항에 가까워 지게 되서 underfit이 될것이다. 따라서 Regularization을 잘 하기 위해서는 적절한 λ\lambda선택 이 중요하다.

Regularized Linear Regression

이전 포스팅에서 선형회귀(linear regression)문제를 풀기위해 Gradient descent알고리즘과 normal equaition알고리즘에 기반한 2가지 해법에 대해서 알아보았다. 이제 두 알고리즘을 Regularization을 어떻게 하는지 알아보도록 하자.

gradient Descent

결과부터 말하자면

Repeat {    θ0 :=θ0−α 1m ∑i=1m(hθ(x(i))−y(i))x0(i)    θj :=θj−α [(1m ∑i=1m(hθ(x(i))−y(i))xj(i))+λmθj]          j∈{1,2...n}}\begin{aligned} & \text{Repeat}\ \lbrace \\ & \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \\ & \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\\ & \rbrace \end{aligned}

가 된다. 그리고 λmθj\frac{\lambda}{m}\theta_j가 regularization을 수행한다.

J는 0을 포함하지 않는데 이는 바로 이전에서 설명했듯이 xnx^n항의 계수를 regularize하기 위함이다. 그리고 θ0\theta_0는 첫번째 식에 의해서 결정된다. 위 식은 아래와 같이 다시 쓸 수 있다.

θj:=θj(1−αλm)−α1m∑i=1m(hθ(x(i))−y(i))xj(i)\begin{aligned} \theta_j := \theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \end{aligned}

위 식에서 1−αλm1 - \alpha\frac{\lambda}{m}는 항상 1보다 작다. 그리고 뒷 부분은 원래 Gradient Descent와 똑같다. 직관적으로 생각했을때 항상 θj\theta_j는 작아진 값으로 업데이트 된다.

Normal Equation

그럼 normal equation의 regularization에 접근해보자. 이전 포스팅 ML2에서 다뤘듯이 normal equation을 반복계산을 하지 않았다.

Normal equation알고리즘 θ=(XTX)−1XTy\theta = (X^T X)^{-1}X^T y

normal equation의 regularization은 행렬 곱을 추가하는 것 외에 원래식과 크게 달라지는것이 없다.

θ=(XTX+λ⋅L)−1XTywhere  L=[011⋱1]\begin{aligned} & \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty \\ & \text{where}\ \ L = \begin{bmatrix} 0 & & & & \\ & 1 & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \\ \end{bmatrix} \end{aligned}

행렬LL는 맨위 안 왼쪽의 항의 0인 diagonal matrix이다.(1이 표시되지 않은 영역은 모두 0이다.) 그리고 주어진 n에 대해서 (n+1)(n+1)(n+1)(n+1)꼴을 띈다.

Non-invertibility 생략

Regularized Logistic Regression

logistic regression에서 특징이 많고 복잡한 다항식 표현에 의해서 과적합이 일어나는 현상을 관찰하였다. Regularizaion의 아이디어를 그대로 가져와서 적용한다면 과적함이 일어아는 복잡한 다항식의 영향이 줄어들게 된다. 방법은 Linear regression에 했던 방법과 비슷하다.

Repeat {    θ0:=θ0−α 1m ∑i=1m(hθ(x(i))−y(i))x0(i)    θj:=θj−α [(1m ∑i=1m(hθ(x(i))−y(i))xj(i))+λmθj]          j∈{1,2...n}}\begin{aligned} & \text{Repeat}\ \lbrace \\ & \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \\ & \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\\ & \rbrace \end{aligned}

Linear Regression 때와 같이 θ0\theta_0에 대해서는 따로 업데이트를 한다. 개인적인 느낌으론 각 알고리즘에 regularization을 적용하는 것보단 Regularization자체의 아이디어를 잘 이해하고 있는것이 더 중요한것같다.

여기까지 Lienar Regression과 Logistic Regression, Advanced optimization 등을 배웠다. 강의를 하시는 Andrew Ng교수님은 여태까지 배운내용을 전부 이해하고 있다면 실리콘벨리에서 머신러닝 알고리즘을 이용해서 떼돈을 벌고 있는 엔지니어들보다 이 강의를 통해 배운 우리가 더 많이 알고있다고 축하와 격려를 해주셨다. ㄷ ㄷ… 앞으로 더 열심히 공부해야겠다는 생각이 든다.

Reference