Coursera에서 제공하는 Machine learning by Andrew ng 을 보고 포스팅하였습니다.

Cost Function

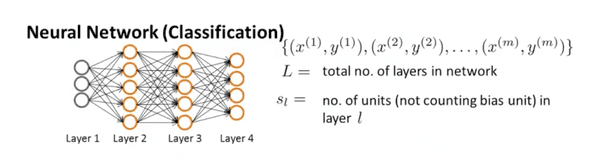
우선 신경망 알고리즘에서 사용하는 몇가지 변수의 정의를 짚고 넘어가자.

• $L$ : 신경망을 이루고 있는 층(layer) 의 총 갯수
  
• $S_l$ : l번째 층에 속해잇는 개체(unit) 의 갯수 (bias unit은 포함하지 않는다.) 마지막 층은 L로 표시한다.
  
• $K$ : 출력 으로 나타나는 개체(units)/클래스(classes)들의 수
  

위 그림에서는 L이 4 s1 = 3, s2 = 5, s2와s4 는 4가 된다. 분류(classification)문제를 풀기위해 신경망 알고리즘을 사용했다고 가정하면

이진 분류 (binary classification)에서는 결과가 하나(0 아니면 1)로 나타나므로 $S_L$은 1이 되고
다중분류(Multi-class classification (K classes))에서는 $S_L$ 은 K가 된다.
(여기서 K는 3보다 크다.)

신경망에서 사용하는 비용함수(cost function) 은 Logistic regression에서 사용했던 비용함수를 변환한것이다. 이전 포스팅 Regularization에서 배웠듯이 Regularized logistic regression에서 사용한 비용함수는 아래와 같다.

위 식에서는 하나의 유닛에 대한 cost function이지만 신경망의 경우 출력 유닛이 k개이므로 이에 맞게 식을 변경해야한다.

시그마가 몇개 더 붙었는데 굉장히 복잡해 보인다…

인공신경망의 결과로나오는 여러 출력노드 k를 포현하위해 몇가지 시그마 연산을 했다. 식의 첫번째 부분 대괄호안의 시그마 연산이 층과 층사이에 거미줄로 연결된듯한 연산을 표현한 것이다.

두번째항은 Regularization항이다. logistic regression의 regularization항과 비고해보면 엄청 복잡해진것 처럼 보이지만 theta matrix의 원소들을 곱한 값을 더하기 위해서 쓴 표현이다.

Backpropagation Algorithm

그렇다면 비용함수의 결과를 최소화하기 위해서는 어떻게 해야할까? Linear regression에서 처럼 gradient descent 알고리즘을 적용했듯이 신경망알고리즘의 비용함수를 최소화하기 위해서는 Backpropagation Algorithm을 사용한다.

이 알고리즘의 목표는 $\min_\Theta J(\Theta)$ 비용함수를 최소화하는 것 이다.

이를 위해서는 $J(\Theta)$와 $\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}J(\Theta)$를 계산해야한다.

이전 포스팅에서 activation values 를 Forward propagation을 통해 계산하였다. 위에서 언급한 미분항을 계산하기 위해서 Backpropagation Algorithm을 사용한다.

Backpropagation Algorithm에서는 모든 노드에 대하여 $\delta$를 계산해야하는데 $\delta$의 정의는 아래와 같다.

• $\delta_j^{(l)}$ = $l$번째 층의 j번째 노드의 “에러” ( $a_{j}^{(l)}$은 l번째 층의 j번째 노드이다. )

그리고 마지막 층에 대해서

로 $\delta$를 구할 수 있다. L은 맨 위에서 정의한 대로 신경망의 가장 마지막층이고 마지막 층에 대한 오류는 실제결과와의 차이므로 간단하게 구할 수 있다.

마지막 층이전의 오류를 구하려면 어떻게 해야할까 마지막에서부터 한 단계씩 앞으로 오면 오류를 구할 수 있다.

l번째 층의 오류 $\delta$는 다음 층의 오류 $\delta^{(l+1)}$과 theta metrix의 곱 그리고 activation function(sigmoid function)의 미분 g’ (지 프라임으로 읽는다.)의 곱으로 구할 수 있다. 그리고 지 프라임 항은 아래와 같이 쓸 수 있다.

이를 이용해서 위의 식을 다시쓰면

가 되고 (증명은 생략합니다.) 이를 정리하면 안쪽 노드에 대한 full backpropagation equation은

위 내용을 정리하면 Backpropagation algorithm

• training set : ${(x^{(1)}, y^{(1)}) \dots (x^{(m)}, y^{(m)}})$
• 모든 $l,i,j$에 대해서 $\Delta^{(l)}_{i,j} := 0$

• t=1 부터 t=m 까지 training example에 대해서

  • $a^{(1)} := x^{(t)}$
  • 층 l = 2,3,4,5,…,L에 대하셔 forward propagation $a^{(l)}$을 계산
  • $y^{(t)}$를 이용하여 $\delta^{(L)} = a^{(L)} - y^{(t)}$를 계산
  • $\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)})\ .* \ a^{(l)}\ .*\ (1 - a^{(l)})$를 이용하여 $\delta^{(L-1)}, \delta^{(L-2)},\dots,\delta^{(2)}$를 계산
  • $\Delta^{(l)}_ {i,j} := \Delta^{(l)}_{i,j} + a_j^{(l)} \delta_i^{(l+1)}$ 혹은 벡터연산 $\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T$

• J가 0이 아니면

  • $D^{(l)}_{i,j} := \dfrac{1}{m}\left(\Delta^{(l)}_{i,j} + \lambda\Theta^{(l)}_{i,j}\right)$

• J가 0이면

  • $D^{(l)}_{i,j} := \dfrac{1}{m}\Delta^{(l)}_{i,j}$

처음봤을 때 이게 알고리즘인지 상형문자인지 모를정도로 복잡한 수식의 나열로 보였다. 앞서 진행한 절차도 하나로 묶는 아이디어도 어려웠다. linear regression이나 logistic regression과 비교해보면 수식적으로나 알고리즘적으로 보나 매우 복잡하다. 하지만 반복적으로 애정을 가지고 바라보고 관련된 문제를 풀다보면 좀더 친숙하게 다가오지 않을까 싶다.

Backpropagation Intuition

Backpropagation 알고리즘이 무엇인지 더 알아보기 위해 비용함수를 살펴보도록 하자.

위의 일반적인 cost function에서 regulartization은 안한다고 하고 ($\lambda = 0$), 그리고 아웃풋이 하나만 있다고 가정하자. 그렇다면 비용함수는 아래 식과 같이 간소화 할 수 있다.

어렵다 나중에 더 포스팅 해야지

reference

• wikipedia - backprogagation algorithm